摘 要:為選擇合理的數控車床切削用量,建立數控車床切削參數能量消耗和加工效率數學模型。在切削參數能量消耗估算模型中,通過實驗擬合與正交實驗分別獲取數控車床的空載功率和切削功率函數,進一步給出數控車床切削階段能量消耗函數。在車床加工條件的各種約束下,設計了一種基于多目標教與學優化算法來求解切削參數能量效率優化模型,以切削階段加工能量最小和加工效率最高為目標,獲得切削參數優化的Pareto前沿解,并采用層次分析法建立了切削參數的決策模型,較客觀地選取了更優車削參數組合。通過數控車床實例優化驗證了所提策略的可行性和有效性。
關鍵詞:車削;能耗;切削參數;教與學優化算法;數控車床
0 引言
數控技術是當今先進制造裝備行業的核心技術,在數控加工過程中合理選擇切削參數可節約能耗和資源、提高生產效率,從而提升企業經濟效益、增強競爭力。然而,目前我國多數數控加工企業還在憑經驗、參考手冊、通過試切來選擇切削參數,往往難以實現能量效率的最優化。隨著現代智能優化算法、切削理論、數學建模和模型分析方法的不斷發展和完善,通過優化切削參數來提高加工效率、減少能量消耗已成為研究的熱點。
對于切削參數優化問題,國內外采用較多的智能優化算法有模擬退火算法[1]、遺傳算法[2]、粒子群優化算法[3]等。也有眾多學者在此基礎上對以上算法進行了改進,例如:CHEN 等[4]在車削參數優化問題中,將Hooke-Jeeves模式搜索與模擬退火算法進行了結合;SRINIVAS等[5]提出了慣性系數隨迭代線性減小的粒子群優化算法來解決車削參數優化問題;SARAVANAN等[6]以最小生產成本為目標,利用模擬退火算法和遺傳算法對車削的切削用量進行了研究;謝書童等[7]提出了基于邊緣分布估計的優化算法,分別采用基因修復與懲罰函數兩種策略解決車削參數優化問題。另外,在切削參數優化模型上也有新的研究,除了將加工成本和工時作為優化目標外,更關注機床的能耗研究,例如:YAN等[8]建立了以能耗、生產率和切削質量為多目標的銑削參數優化模型,首次將切削能耗考慮在內,利用灰色關聯分析和曲面響應法對其進行了尋優;李聰波等[9]利用復合形法,以高效低碳為多目標進行了切削用量的尋優,并通過實例驗證了模型的有效性;李建廣等[10]緊接著也從能量消耗的角度對切削參數進行了優化,考慮了機械加工對環境的影響。可見,機械加工切削參數的能量效率優化研究已經越來越受到研究者的重視。
當前,求解切削參數優化的問題大多采用元啟發式優化算法,然而這種算法的參數設置對求解結果有較大影響。近年來,一種高效、可屏蔽參數干擾的教與學優化算法受到研究者的廣泛關注;基準函數實例測試顯示,該算法比遺傳算法和粒子群優化算法能獲得更高質量的解[11]。本文首先通過正交實驗給出數控車床切削階段的能量估算函數,設計一種改進多目標教與學優化算法解決切削參數的能量效率優化問題,采用層次分析法選擇更合理的切削參數,實現切削用量從定性的隨機選取到定量選取,并通過實例優化驗證了所提策略的可行性。
1、 數控車床能量效率模型
在數控車床切削過程中,切削三要素是影響加工過程能量效率的關鍵因素。為減少加工能耗、提高加工效率,選擇合理的數控車床切削用量,建立數控車床切削參數的加工能量和加工效率數學模型。
1.1 加工能量數學模型
數控機床加工過程涉及待機狀態、空載狀態和切削狀態,由劉飛[12]等對機床的研究理論可知,當系統處于切削狀態時,機床的總功率損耗包括空載功率損耗Pu、切削功率損耗Pc和附加載荷功率損耗Pa。目標函數是優化變量的函數,是評價和選擇優化切削用量的指標。本文所考慮的機床加工過程的功率損耗均與切削三要素有關,故第一個目標為:
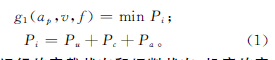
在機床運行的空載狀態和切削狀態,機床的空載功率均對機床的功率損耗有較大影響。同樣地,劉飛等[12]指出,只有當機床空載功率與主軸轉速n近似呈二次函數變化關系時,才能準確地反映其損耗功率的構成,機床空載功率可通過實驗擬合得到:
![]()
對于負載時的附加載荷損耗功率Pa,其附加損耗機理十分復雜,一般無法通過理論計算準確獲得其函數關系,劉飛等[12]指出其附加載荷損耗與載荷損耗呈近似的線性比例關系,比例系數α 的取值范圍一般為0.15~0.25。

通過正交實驗設計可以獲得切削功率與切削參數之間的指數經驗模型關系。采取三因素三水平正交實驗設計,每個切削參數被編碼為-1,0,1三個水平,分別按式(5)進行編碼,對式(4)取對數簡化后,可以得到切削參數和響應值的編碼關系(式(6))。
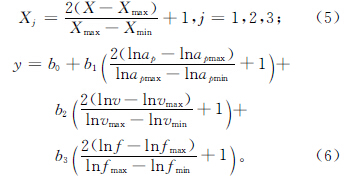
對上式進行變量分離,可得到系數和指數關于回歸系數bi(i=0,1,2,3)的代數式,而4個回歸系數可根據矩陣原理計算求出:
![]()
式中:X 為切削參數的編碼矩陣,A 為對角陣,B 為回歸系數矩陣,從而可以通過矩陣原理求出切削功率Pc指數模型中的各項系數和指數,得到總加工能量的數學模型。
1.2 加工效率時間數學模型
切削時間即為加工時間的一部分,均可反映機床的加工效率,即加工時間短、機床的生產率就高,在保證加工質量的前提下,這也是現階段各數控裝備企業追求的目標之一。其中加工工時可以分為實際切削時間、換刀時間以及輔助時間三部分,其準確表達式為:
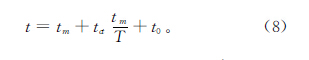


1.3 約束條件
切削用量的取值受諸多因素約束,主要有切削參數自身的范圍約束、機床性能約束和加工質量約束等,數控車床的切削參數只能在約束條件的范圍內進行尋優。
(1)機床切削速度約束
主軸轉速必須在機床允許的最小轉速和最大轉速之間,而轉速與切削速度之間可相互轉換。對某一特定數控車床而言,其正常轉速有一個具體范圍,當加工工件的直徑D 確定時,可以得到切削速度的范圍:

(3)機床背吃刀量約束
背吃刀量取決于刀具材料、工件材料和車床允許的最大切削力。背吃刀量也與加工工藝有關,一般地,進行粗加工的背吃刀量相對較大,但加工表面無要求。本研究中對加工表面有較高要求,故背吃刀量的選擇在半精加工的范圍內取值:
![]()
(4)機床功率約束
加工過程所消耗的功率必須在機床所能提供的最大有效切削功率范圍內。最大有效切削功率Pcmax直接受機床主電機功率約束,機床主電機功率和機床的傳動系數η則由數控車床決定:
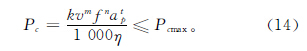
(5)切削力約束
加工過程中刀具與工件接觸,所產生的切削力需進行約束。其中:主切削力最大,背向力和進給力均小于主切削力,主切削力必須在最大允許切削力范圍內,其值可通過查表獲取:
![]()
(6)表面粗糙度約束
切削用量直接影響已加工表面的粗糙度,優化的切削用量也必須滿足表面粗糙度的約束。粗糙度可按加工要求獲取,刀尖圓弧半徑rε由車刀決定:
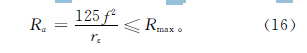
綜合以上目標函數和約束條件,得到該數控車床切削參數的多目標優化數學總模型:
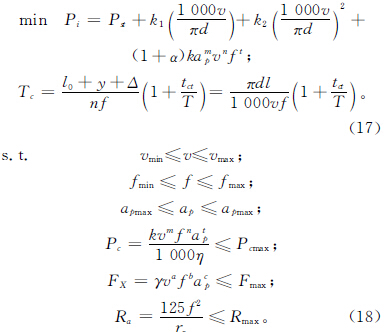
2 、多目標教與學算法求解切削參數優化問題
2.1 改進的教與學算法
教與學優化算法是Rao等于2010年提出的一種新的群智能優化算法,該算法的參數少、操作簡單、易理解、求解速度快、精度高且具有極強的收斂能力[11]。本文設計了一種改進多目標教與學優化算法,以解決切削參數能量效率優化問題,算法求解過程如下:

(2)教階段 首先根據設定的最小偏優策略在學生群體中選取一位老師Xteacher,然后班級中每個學員根據Xteacher和學員各科目的平均值mean之間的差異性進行學習。
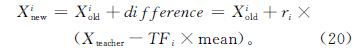
式中學習步長ri=rand(0,1)。考慮到在實際學習時,學員根據自己的接受能力向老師學習,學習能力強則學習較快,學習能力弱則學習較慢[13],因此教學因子采取自適應的模式為:

(4)自學階段 在實際中最主要的學習方式是自學,是自己和自己比較,增加自學方式可以使學員的學習形式更加多樣化,從而使算法的全局搜索能力更強,其自學方式為:
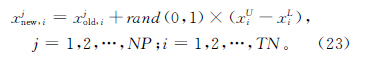
2.2 切削參數優化過程
班級中學員數為種群大小NP,學員需要學習的科目為切削三要素,即任務數TN=3。目標函數為學員的學習成績,作為切削參數選取的重要指標。對于模型中約束的處理,在學員初始化時,首先在切削三要素范圍內隨機生成班級學員的科目值,縮小尋優范圍。對于主切削力、最大切削功率以及加工質量的約束,在教、學以及自學階段結束后進行過濾處理,對于過濾后的學員,其切削三要素重新在約束范圍內生成,重構班級學員。
非支配解集的構建是通過Pareto排序實現的,設定一學員的加工能量和加工效率均小于另一學員才被該學員支配,否則為非支配解。然后對非支配解進行排序,得到排序為1的即為非支配解集,該解集中的任一學員均不被其他學員支配,而所尋求的多目標最優解在其構成的Pareto前沿解集上。
在教階段,首先對初始解進行約束過濾處理,然后進行Pareto排序,學生向老師學習,需要找出一個Xteacher。本文的研究目標是對切削參數進行尋優,要求需同時滿足機床功率損耗和切削時間達到平衡狀態的較小值,因此,算法加入了最小偏優策略進行改進,即學員各科目成績與對應的全班各科目最優成績的偏離總和最小的學員作為學習對象。對于Pareto排序為1的學生,計算每個學生的目標值和最小目標值的相對誤差平方和:

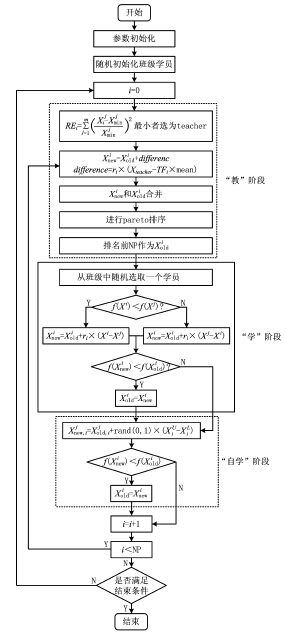
教學工作完成后,將得到同樣多的新學生,這些學生中理論上存在比之前更差的學生,然后合并新學生和舊學生的成績,統一排序后,取成績排名為前班級人數的成績所對應的學員作為新的學生群體。在學階段,從班級中隨機選取一個學員進行相互學習,若成績提高則替換,否則繼續保留原學員。自學階段和學階段類似,只是學習對象有所不同,此時學習對象變為自己,學習的過程相同。結合本文的研究目標,改進的多目標教與學優化(Teading-Learning-Based Optimization,TLBO)算法實現的流程圖如圖1所示。
3、 優化實例驗證
3.1 切削能量模型實驗與驗證
3.1.1 空載功率擬合
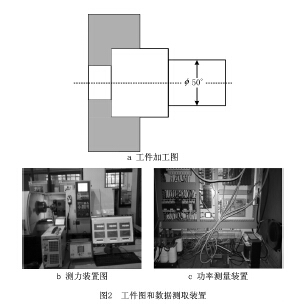
通過CK60數控車床配備華中數控系統進行切削加工實驗,工件(45#熱軋鋼)切削長度為100mm,直徑為50mm,如圖2a所示;采用Kistler測力儀以及NI虛擬儀器采集切削力信號(如圖2b),可獲得三向切削力大小,車刀采用主偏角45°的涂層硬質合金刀具MSSNR2525M12;另外,待機功率和空載功率均由WB9128三相功率傳感器測取,如圖2c所示。
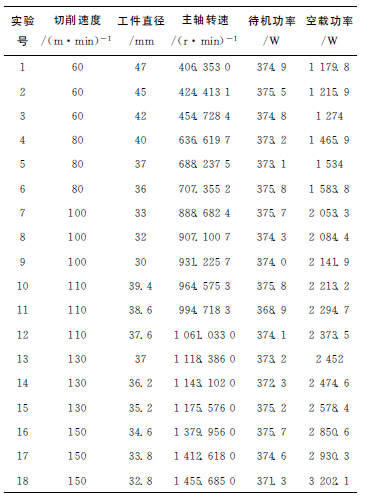
為研究機床空載功率和主軸轉速的關系,進行了18組實驗,轉速為145r/min~1 500r/min,主要根據不同切削直徑對應的切削速度轉化而成。切削的同時,功率傳感器采集主軸轉動前后的信號,得到如表1所示的待機功率和空載功率。
表1 空載功率實驗數據
用MATLAB進行二次擬合,得到如下空載功率與主軸轉速的二次關系式:
![]()
從擬合結果中不難看出,轉速二次項對空載功率損耗的貢獻系數較小,可見在該實驗條件下,空載功率基本與主軸轉速呈線性關系。對其進行方差檢驗R2=0.98,F=373>F0.05(2,15),擬合效果甚佳。另外,最低空載功率即為轉速為零時的功率,與試驗中的待機功率非常接近,進一步說明該二次擬合的準確性,因此關于主軸轉速的二次型可以有效且準確地預測相應的空載功率損耗。
3.1.2 切削功率估算
切削功率可以通過扭矩傳感器或者測力儀間接獲取,本實驗采用Kistler測力儀以及NI虛擬儀器采集切削力信號,測取X 和Z 向切削力,由下式間接獲取切削功率,其測力裝置如圖2b所示。
![]()
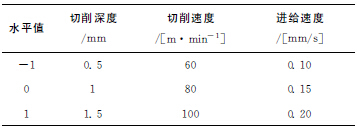
由于三因素均對切削功率有較明顯的影響,若采用普通實驗,則需大量的數據才能得到較好的結果。本實驗采用三因素三水平的正交實驗設計,其正交試驗結果如表2所示,表3為對應的參數編碼。
表2 正交試驗表
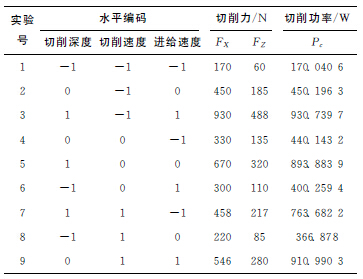
表3 各水平值對應的參數設置

同理,為了總模型中主切削力的約束,主切削力FX的指數模型如下:
![]()
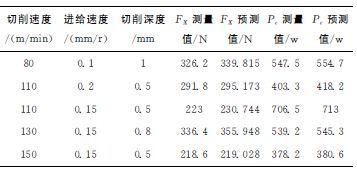
另外,進行了5組實驗來驗證以上模型,結果如表4所示,其中主切削力FX的預測誤差為3%,而實際切削功率的預測誤差僅為1.5%,二者均在誤差可控范圍之內,所得模型具有較高的預測精度。
表4 模型驗證實驗數據
因此,結合以上在實驗基礎上獲取的空載功率和切削功率模型,切削階段總能量模型如下:
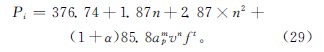
3.2 切削參數能量效率多目標優化
3.2.1 切削參數優化
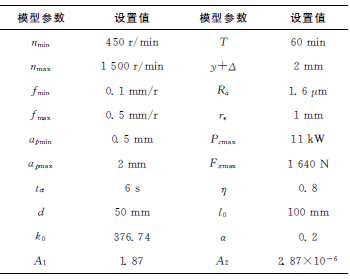
改進的TLBO算法使用C++語言編譯,運行于Windows 7操作系統,單核英特爾酷睿CPU,2GB內存。其模型中的各參數設置如表5所示,算法中的種群大小NP=50,最大迭代次數為200代。
表5 模型參數設置表
該算法最后得到了17組Pareto前沿解,其中第1組和第17組分別具有機床功率損耗最小和切削工時最小的兩個極限值,其他均在二者之間,無傳統意義上的最優解。為證明改進的TLBO算法具有更優的效果,將其與經典多目標進化算法快速非支配排序遺傳算法(Non-dominated SortingGenetic Algorithm,NSGAII)進行了比較,在同樣的種群大小和迭代次數下,NSGAII得到了11組非支配解,非支配解的分布也不及改進的TLBO算法。另外,其Pareto前沿均在本文所提出的改進的TLBO算法之上,而目標為機床功率P 和加工工時T 均取小值,故NSGAII得到的Pareto解均被其支配,這表明了改進的TLBO算法在得到最優解方面表現出了很強的搜索能力,其Pareto圖如圖3所示。在此曲線上的點均可作為較優解,后文將用層次分析法進行決策,得到折衷最優的切削用量。
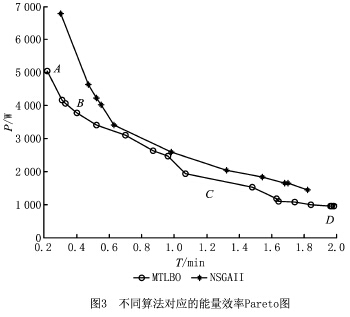
3.2.2 切削用量對加工能量效率的影響分析
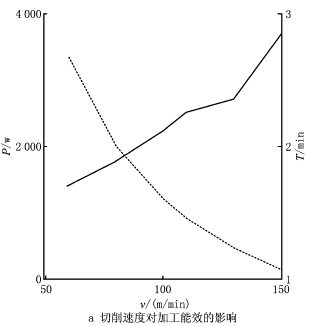
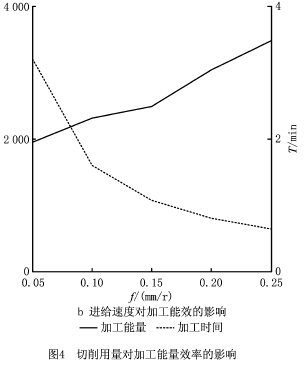
切削用量是影響加工過程能量效率的重要因素,當f=0.1mm/r和ap=0.5mm時,切削速度對加工能量效率的影響如圖4a所示,隨著切削速度的增加,切削階段的能量消耗不斷增加,加工時間不斷減小。當v=100m/min和ap=0.5mm時,進給速度對加工能量效率的影響如圖4b所示,隨著進給速度的增加,切削階段的能量消耗不斷增加、加工時間不斷減小。可以看出,二者對切削階段的能量消耗和加工時間的影響趨勢一致。當然,當切削速度和進給速度一定時,隨著背吃刀量的增加,切削力增大,導致切削階段消耗的功率增加,而加工時間長短和背吃刀量無關。然而,在選擇車床切削用量時,切削三要素之間具有內聯性,當背吃刀量增加時,為防止切削力和消耗功率過分增加,必然會影響進給速度和主軸轉速的選取,從而影響加工時間的長短。
3.3 切削參數決策分析
3.3.1 切削參數選擇
為了在17組Pareto前沿解中找出最優的一組解,采用層次分析法決策,將這17組解作為方案層,將兩個目標函數所得的值作為準則層,采用層次分析法的目標就是確定一種最優參數組合,即目標層。該方法將定量分析與定性分析結合起來,利用決策者的經驗,采用1~9的標度判斷各衡量目標能否實現的標準之間的相對重要程度,并合理地給出每個決策方案的標準的權數,利用權數求出各方案的優劣次序,從而選擇出更優的切削參數組合。
由Pareto圖可以看出,機床功率損耗和實際切削工時是一對互逆的準則,不可能同時達到最優,若要得到一組相對更優的解,應該對其折中取值。因此,將Pareto解集曲線進行分段,對BC段的6組參數采用層次分析法進行決策。
按照判斷矩陣元素的標度方法可以得到方案層對準則層的成對比較矩陣P 和T 以及各矩陣所對應的最大特征值分別為6.122 5和6.273 2。

將機床功率損耗與實際切削工時進行對比,顯然機床功率損耗比實際切削工時對方案的選擇影響大,因此取其稍微重要,即有準則層對目標層的權向量W2=[0.75,0.25]T,其一致性指標CI=0,通過一致性檢驗。另外,求出P 和T 的最大特征值對應的特征向量后,歸一化處理即為各方案對各準則的貢獻程度,即方案層到準則層的權向量W1,最后得到層次總排序W,
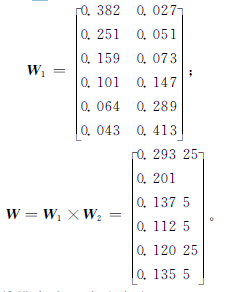
層次總排序的一致性檢驗:CR=0.026<0.1,通過一致性檢驗,可以得到第9組的權重最大,即綜合考慮兩個目標且滿足各項約束條件時,第9組的參數組合相對最優。
3.3.2 結果分析
當切削直徑為30mm的工件時,將第9組最優切削用量組合按機床轉速表和進給量表規范得到轉速n=900r/min,進給量F=170mm/min,ap=0.5mm,進行實驗驗證最后得到機床功率損耗為1 964W,實際加工時間為65s。由切削原理可知,由于半精加工時切削深度較小,產生的切削力也較小,可在保證表面粗糙度的前提下適當加大進給量,可以看出改進的TLBO算法在多目標優化中應用的結果符合切削參數的選擇原則。因此,采用本文所提改進的TLBO算法可以有效地選擇出切削用量。
4 結束語
為合理選取數控車床切削用量,本文建立了數控車床的加工能量效率模型,采用改進的基于Pareto排序的多目標TLBO算法進行尋優,對Pareto前沿解采用層次分析法進行決策,得到了最優切削參數組合。可以看出,合理切削用量的選取受到機床自身多個因素的影響以及加工要求的約束,通過分析切削參數對機床加工能量以及加工效率的影響,切削用量的選取具有內聯性。本文主要針對數控車床車削加工切削參數能量效率優化,對數控機床能耗的影響分布以及多源能量流特性的研究將是未來的重點研究方向。
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com




