基于 MATLAB 的插床機構(gòu)運動學(xué)和動力學(xué)規(guī)律分析
2019-9-17 來源: 河南理工大學(xué) 機械與動力工程學(xué)院 作者:吳雪峰 張惠陽 張洪銘 范玉
摘 要: 插床導(dǎo)桿機構(gòu)作為一個典型連桿機構(gòu),其運動學(xué)和動力學(xué)分析具有很強的代表性。 通常可利用圖解法對插床導(dǎo)桿機構(gòu)進行分析,由于手工繪圖過程繁瑣,求解精度有限,很容易產(chǎn)生誤差。 采用矢量解析法對插床導(dǎo)桿機構(gòu)進行分析,利用矩陣法求解,不僅求解精度高,而且通過繪出機構(gòu)相應(yīng)的運動和動力線圖,能形象快速的表達出原動件轉(zhuǎn)動角度和各構(gòu)件運動和動力特性之間的關(guān)系,具有很大的優(yōu)勢,便于機構(gòu)的優(yōu)化設(shè)計。
關(guān)鍵詞: 插床; 運動學(xué)分析; 動力學(xué)分析;連桿機構(gòu)
0 引言
插床主要用來槽類特征加工。 加工時工作臺上的工件做縱向、橫向或旋轉(zhuǎn)運動,插刀做上、下往復(fù)運動,切削工件。 插床主要由齒輪機構(gòu)、導(dǎo)桿機構(gòu)和凸輪機構(gòu)等組成。 插床導(dǎo)桿機構(gòu)即插床主運動的機構(gòu),由曲柄滑塊為基礎(chǔ)拓展而成,以低副連接形成的單自由度連桿機構(gòu)。
對插床的導(dǎo)桿機構(gòu)運動學(xué)分析和動力學(xué)分析有利于對插床工作性能的把握。 其分析方法分為圖解法和解析法,圖解法能簡單地呈現(xiàn)機構(gòu)的某一個或某幾個位置的運動和動力特性,精度滿足實際問題的要求。本文利用矢量方程解析法,分析原動件旋轉(zhuǎn)角度與刀具的位移、速度、加速度,在此基礎(chǔ)上確定出各鉸支座受力以及平衡力矩之間的聯(lián)系,進而得到機構(gòu)整個運動循環(huán)過程中的運動學(xué)和動力學(xué)特性,為后續(xù)機構(gòu)強度和機構(gòu)形狀設(shè)計奠定穩(wěn)固的基礎(chǔ)。
1 、插床導(dǎo)桿機構(gòu)的運動學(xué)分析
插床導(dǎo)桿機構(gòu)簡圖如圖 1 所示,該插床導(dǎo)桿機構(gòu)的工作過程可看作原動件 O2A 桿以等角速度做定軸轉(zhuǎn)動,并且?guī)訌膭蛹?AB 桿和 BC 桿做平面運動,最后再帶動插刀 5 沿導(dǎo)路做上、下往復(fù)運動,對工件進行切削。
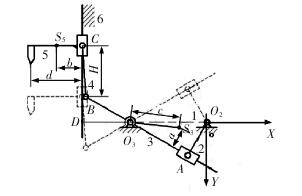
圖 1插床導(dǎo)桿機構(gòu)簡圖
(1)位置分析在圖 1 所示的機構(gòu)簡圖中,以 O2為原點建立直角坐標(biāo)系,并標(biāo)出各桿矢量及其方位角。利用三角形O2O3A 和四邊形 O3BCD 兩個矢量圖形 ,分別建立矢量方程為:

由式(3)和式(4)即可求得導(dǎo)桿 3 的方位角和滑塊 2 在導(dǎo)桿上的位置,代入式(5)和(6),即可求得連桿 4 的方向角和插刀 5 的位置。
(2)速度分析將式(3)~式(6)對時間求一階導(dǎo)數(shù),并寫成矩陣形式,即得到以下速度矩陣
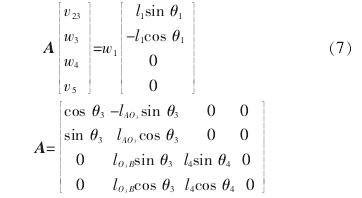
通過式(7)可得到刀具的速度 v5和構(gòu)件 2 的相對速度 v23,構(gòu)件 3 的角速度 w3和構(gòu)件 4 的角速度 w4。(3)加速度分析對式
(7)對時間求一階導(dǎo)數(shù),便得到加速度矩陣

表 1 機構(gòu)尺寸及構(gòu)件重量
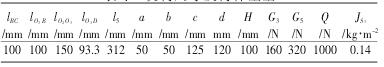
插床導(dǎo)桿機構(gòu)中的滑塊的運動即是插床中刀具的運動,導(dǎo)桿機構(gòu)尺寸及各構(gòu)件重量如表 1 所示,利用 MATLAB 軟件計算得到滑塊的運動學(xué)分析曲線如圖 2 所示,得到刀具的速度最大為-0.204 m/s(負(fù)號表示方向向上),加速度最大為+0.613 m/s2(正號表示與此時速度方向相同)。 刀具在變速運動中產(chǎn)生的加速度會引起慣性力,在刀具加工過程中,此慣性力對刀具產(chǎn)生柔性沖擊,因此在刀具的選擇上還要考慮到柔性沖擊的影響。
2 、插床導(dǎo)桿機構(gòu)的動力學(xué)分析
插床對工件進行切削加工,其對力的要求相對較高,同時機構(gòu)的約束反力是進行強度分析的基礎(chǔ)。由導(dǎo)桿機構(gòu)的運動學(xué)分析得到各構(gòu)件的相關(guān)構(gòu)件質(zhì)心角速度和加速度,可求出構(gòu)件 3 和構(gòu)件 5 的慣性力F13和慣性力偶矩 M15。
在用矩陣法對導(dǎo)桿機構(gòu)進行分析時,通過建立以 O2為原點的平面直角坐標(biāo)系,然后分別對各個構(gòu)件列出力平衡方程,對于構(gòu)件導(dǎo)桿機構(gòu)中任一活動構(gòu)件 i,都列出 3 個力平衡方程式,因此導(dǎo)桿機構(gòu)可列出 15 個力平衡方程式,得到各運動副的約束反力如圖 3 所示。
由圖 3 可以分析出,當(dāng)切削阻力發(fā)生變化時,各鉸支座約束力也會發(fā)生迅速變化,切削阻力延 Y 軸正方向,因此各鉸支座 Y 軸分力相對于 X 軸分力更大。
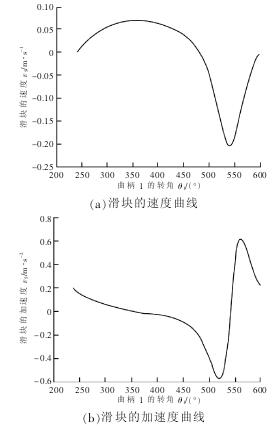
圖 2 滑塊的運動學(xué)分析曲線圖
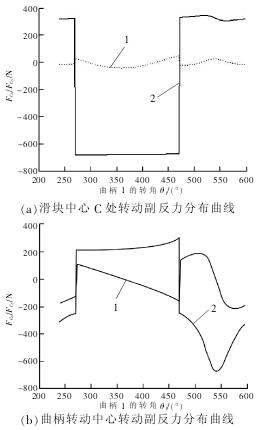
圖 3運動副反力曲線1. FCx2. FCy
3 、利用動能定理求解平衡力矩
由于在一個工作循環(huán)中,刀具受力變化將引起主軸的速率波動,需要用飛輪調(diào)速,減小電機容量和提高切削質(zhì)量。 平衡力矩是選用飛輪轉(zhuǎn)動慣量的重要依據(jù)。 本文利用動能定理求解,可避免對于各約束反力求解,簡化計算過程。該導(dǎo)桿機構(gòu)的運動方程式為
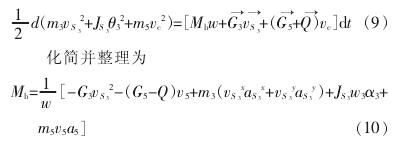
運用動能定理求解平衡力矩不需要展開為矩陣,進行復(fù)雜的運算,可以直接帶入 MATLAB 程序中,得到相應(yīng)的數(shù)據(jù)結(jié)果。 其平衡力矩Mb曲線圖如圖 4 所示。
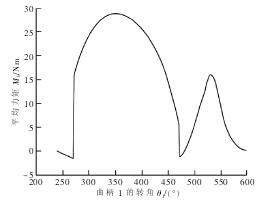
圖 4平衡力矩曲線圖
由圖 4 可以分析出,當(dāng)切削阻力變化時,平衡力矩也會發(fā)生迅速變化。 其中平衡力矩最大值為28.88 Nm,最小值為-1.43 Nm。
4 、結(jié)語
為得到插床導(dǎo)桿機構(gòu)運動學(xué)和動力學(xué)規(guī)律,本文首先對插床導(dǎo)桿機構(gòu)進行運動學(xué)分析和動力學(xué)分析,建立其矢量模型,然后利用 MATLAB 軟件的矩陣運算功能,獲得其運動和動力特性,并將結(jié)果可視化,獲得插刀的位移、速度、加速度、以及各構(gòu)件的約束反力隨原動件轉(zhuǎn)動角度變化的規(guī)律,最后,利用動能定理求出平衡力矩。 上述分析方法為插床導(dǎo)桿機構(gòu)的優(yōu)化設(shè)計奠定理論基礎(chǔ),同時也為其他連桿機構(gòu)進行運動學(xué)和動力學(xué)分析提供了很好的借鑒。
投稿箱:
如果您有機床行業(yè)、企業(yè)相關(guān)新聞稿件發(fā)表,或進行資訊合作,歡迎聯(lián)系本網(wǎng)編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業(yè)、企業(yè)相關(guān)新聞稿件發(fā)表,或進行資訊合作,歡迎聯(lián)系本網(wǎng)編輯部, 郵箱:skjcsc@vip.sina.com
更多相關(guān)信息
業(yè)界視點
| 更多
行業(yè)數(shù)據(jù)
| 更多
- 2025年6月 新能源汽車銷量情況
- 2025年6月 新能源汽車產(chǎn)量數(shù)據(jù)
- 2025年6月 基本型乘用車(轎車)產(chǎn)量數(shù)據(jù)
- 2025年6月 軸承出口情況
- 2025年6月 分地區(qū)金屬切削機床產(chǎn)量數(shù)據(jù)
- 2025年6月 金屬切削機床產(chǎn)量數(shù)據(jù)
- 2025年5月 新能源汽車銷量情況
- 2025年5月 新能源汽車產(chǎn)量數(shù)據(jù)
- 2025年5月 基本型乘用車(轎車)產(chǎn)量數(shù)據(jù)
- 2025年5月 軸承出口情況
- 2025年5月 分地區(qū)金屬切削機床產(chǎn)量數(shù)據(jù)
- 2025年5月 金屬切削機床產(chǎn)量數(shù)據(jù)
- 2025年4月 新能源汽車銷量情況




